
What’s the best way to explain the times tables without just repeating them over and over?
How Can I Teach My Child the Times Tables Without Just Going Over and Over Them?
For some children, learning a sequence of anything can prove tricky. Others may learn a rhyme by rote (e.g., the alphabet song or 5, 10, 15, 20, etc.) but can’t actually answer a question when asked. Others can only get to the answer by going through all the previous questions first.
So, how can you explain times tables to someone without just repeating them again and again?
I think the best place to start is by looking at how we learn.
If you'd rather watch a video version of the article click here
How do we learn?
Learning is unique to each one of us. However, there are some principles we can use to support any child’s education that will prove beneficial.
If we give our children something to do to help them learn, we help them create a memory. For a younger child, this might be flashcards to help them recognise basic words, which can then be built upon to help them learn to read.
For an older student, we may give them a worksheet to help them learn non-linear simultaneous equations.
In doing so, we help them create a memory in their brain where they can go to recall that piece of information.
(I’ve used those two examples to show how this is relevant to all levels of students.)
We then play with the flashcards again or give them another worksheet. In doing so, we help reinforce that memory — to make it stronger.

Learning is unique to each one of us. However, there are some principles we can use to support any child’s education that will prove beneficial.
However, when they are in the classroom and the teacher asks them a question, or they are in a test and their brain goes into a state of panic, they may be running around inside their brain trying to find the information they need, no longer thinking rationally. The chance of them picking up on that one memory is limited.
Yet, if we give them a second activity to help them learn, it will support them in creating a second place in the brain where they can find this information. Instead of using the flashcards, we might write those same words onto Jenga bricks so that, as you take one from the tower, you must read it before replacing the brick onto the top for the other person to have a go. Or create a pairs game where you match the words to a picture, or a word to a word. You might play bingo, draw images of the words and write the word next to it, make the words out of magnetic or Scrabble letters, or write them in the sandpit or with water on the side of the building.
For the student learning non-linear simultaneous equations, you might ask them to create a poster using large bright colours explaining to their peers how to solve these problems. Or you might create a board game where you need to answer the questions as you go. Code breakers offer another alternative.
The goal is to make the activities as interactive as possible. Use colours — ideally a minimum of five — as this helps open different neural pathways.
This approach also aims to make learning enjoyable. If the child is relaxed, they are more likely to take on the information rather than focusing on the desire not to be doing it.
Furthermore, if they are enjoying themselves, they will be more likely to want to participate — and with participation comes practice. With practice comes ability, and with ability comes confidence. It becomes a positive spiral of success.
The goal is to make the activities as interactive as possible.
Use colours, ideally a minimum of 5 as this helps to open different neuro pathways.
This approach also aims to help make learning enjoyable. If the child is relaxed, they are more likely to take on the information that they are given rather than focusing on the desire not to be doing this.
Furthermore, if they are enjoying themselves, they will be more likely to want to participate and with participation comes practice. With practice comes ability, with ability comes confidence and it becomes a positive spiral of success.
Use playdough to shape letters or numbers. It is more engaging than writing on paper, and it helps create stronger, more lasting memories.
Use physical resources to help
Some children may benefit from using physical objects to sort into groups. For example, if you are working out 5x8 you can explain to them that this means that there are 5 groups with 8 in each. Encourage them to count out these 5 groups and then count the number of items there are in total. You can literally use anything for this: pens, Lego, counters, books (if you have enough), teddies, Sylvanian family figures, or even smarties. Your options are limitless!
Give all the support that they need to help them to succeed
I often use the analogy of when a baby first starts to learn to walk. We hold both their hands, and we are there with them every step of the way. We praise every step and celebrate it out loud, with pure and genuine pride.
Then slowly they gain confidence, and they let go of one of our hands.
We are in awe of what they are doing, but we remain closely by their side holding that other hand just in case they need us.
Then one day they let go altogether and they no longer need us. They have the confidence and the ability to walk, to run without us. From that moment, they never look back.
Academic learning is no different. We need to provide that safety net whilst it is needed.

Offer all the support that they need
Remember that everyone learns differently, we are all unique individuals.
Most of the times tables also have a range of tricks
These tricks will help us to support a child in learning the times tables. I wouldn’t suggest working through them in chronological order as by doing so you will encounter many of the harder times tables, prior to doing the easy ones.
What order should we learn the times tables in?
So, start with the simple ones, ensure you child is completely confident with this one and then move on. There is no rush. Slow and steady. Learning most things is like a marathon rather than a quick sprint. Taking your time is far more effective than diving into the quickly, losing confidence as things are moving on to quickly and either quitting or having to go back over old ground.
Prior to beginning make sure your child is comfortable with the terminology that they might encounter when multiplying, timesing, groups of, using multiplication, etc. (When I tried to Google a comprehensive list to give you it came up with over 500).

How to support the 2x tables:
Starting with the 2x table seems to be the most common place to start. I would suggest that this is because they are possibly used to adding 2 of the same number together by the time that they start to familiarise themselves with the 2x table. So, in order to multiply by two they are simply doubling numbers.
To compliment this idea, I would start by using physical objects (or dots) to work out the answers. Then using colours (get as creative as you can) create a poster with all of the questions and answers written on it. I would suggest you do this for all of the times tables. You could buy one, but your child will be far more likely to recall the information if you let them create it.
Then, as implied before, keep it by their side for as long as they need the reassurance. I would also suggest that you make the questions and answers from playdough or similar (they are simple recipes to make your own online, I think you just need to mix flour, water, salt and colouring if you choose). Write them with water or in gloop (a baking powder and water mix) whilst they gain confidence. It’s fun, multisensory, but also if they get it wrong it will dissolve and be eliminated rather than remaining as a lasting memory.
Always offer praise when they do well.
(Each of these ideas can be replicated when practising any of the times tables)

How to support the 10x tables:
The 10x table is a firm favourite. To make something “10x bigger” move the decimal point along one space.
Pardon?
To multiply any whole number by 10, put a zero on the end.
It’s as simple as that.
6x10=60
60x10=600
1,000x10 = 10,000

How to teach the 5x tables:
The 5x table once again has a simple pattern to it. When you multiply an odd number by 5, the answer will end in a 5. When you multiply an even number by 5, the answer will end in a 0.
In other words, the pattern will go 5,0,5,0,5,0, and so on.
Although this is a simple pattern, most children will learn it best by going through the motions of counting in 5’s until they get to the number they need. Make sure that they stop in the right place. So many people get carried away by their skill in counting that they forget to stop and then realised they have gone too far, needing to start again.
The 5’s are quite easy but will probably be cemented into their minds more as they become more confident with the other times tables.

How to support the 11x tables:
I love the 11x tables!
When multiplying by 11 you are in effect multiplying by 1, twice. 1 in the 1’s column and a 1 in the 10’s column. When you multiply by 1, the answer is just itself. So knowing that, 4x11 will be 44. 8x11 is 88.
The problem begins when you get to double digits, because 11x11 is not 1111.
However, I lad I worked with a year or two back taught me that if you:
Split the number you are multiplying together 11x11 (write the 11 with a gap in the middle 1 1)
Next add the digits in the number you are multiplying by 11 together (1+1 =2)
Put the answer to step 2 in the gap created in step 1: 121
11x11=121!
That blew my mind!
Let me give you an example with slightly clearer digits. Let’s go 35 x11.
Split the number you are multiplying together 35x11 (In this instance write the 35 with a gap in the middle 3 5)
Next add the digits in the number you are multiplying by 11 together (3+5 =8)
Put the answer to step 2 in the gap created in step 1: 385
35x11=385
Just to check:
35x10=350
350 plus another group of 35 (350+35) = 385.

How to support the 9x tables:
This begins to get slightly more difficult at this point, but the 9 times table has multiple tricks that you can use to help you to learn it.
If you write down the answers to the 9 times table, you will notice that as you move down the tens column the number increases by 1 each time and the unit column decreases by 1 each time:
09
18
27
36
45
54
63
72
81
90
99
108
Additionally, each of the digits in the answers of the 9x table add to 9 so it's a quick and easy way to check if you're right or not:
6 x 9 = 54
5+4 = 9,
2 x 9 = 18
1+8=9,
12 x 9 = 108
1+0+8=9.
You also have the finger rule for the 9x table:
If I ask you what 4 times 9 is, you could work this out by laying down the 4th finger on your left hand. To the left of that finger, you have 3 fingers standing up; these are your 3 tens.
To the right you have 6 fingers standing up. These are your units.
3 x 9 therefore is 36.
This works with all the numbers in the 9x table from 1 to 10.
Another example might be 8 x 9:
Put my 8th finger down. To the left I have 7 ten's and to the right I have 2 units.
Therefore, the answer is 72.
Another brilliant trick I was taught is easier to explain with an example:
7x9
Subtract 1 from the number you are multiplying by 9
7-1 = 6
So, our answer will start with a 6.
Now we need to work out, what we would need to add to 6 to get to 9?
6+3=9 (or 9-3=6)
So, the answer to 7x9 =63
Another example could be 4x9
4-1=3
3+6=9
4x9=36!
There are so many tricks to help with the 9x table, so although it is one of the higher numbers, it is actually easier than some of the others such as the 7’s.

If you write down the answers to the 9 times table, you will notice that as you move down the tens column the number increases by 1 each time and the unit column decreases by 1 each time:

The finger rule for the 9x tables
Unfortunately, we have done most of the easier times tables now. However, we can use the knowledge from what we have learned to help us moving forward. For example, we don’t know our 6 times table but if we were asked 5x6 we could swap it around and work out 6x5 as we already know our 5’s.
From here on, you could start to work on them in any order, but I will work through them in chronological order just for ease of reference.

How to support the 3x tables:
The 3x table is harder than the previous ones as there are no real patterns to help to with calculating the answers, however a trick that might prove useful is the knowledge that any answers in the 3x table, the digits in the answer will always add to a number in the 3x table.
Let me give you a couple of examples. The times table starts with 3,6,9,12, etc
7x3= 21
2+1=3, so 21 is the correct answer
9x3=27
2+7=9.
We can see from above that 9 is in the 3 times tables so 27 is the correct answer.
11x3=33
3+3 is 6, again we can see from above that 6is in the 3 times tables so 33 is the correct answer.
Although it won’t help us to get to the answer, this will help us to check our answers.
I would suggest that, as with the 2’s you use physical objects to help you to group things and work out the answers until you are confident with the 3’s if necessary.

How to support the 4x tables:
By now we are confident with our 2x table. Because of this I will suggest that to work out the answer for the 4x table, simple multiply the number by 2 and then double it/multiply it by 2 again.
So, is we are asked what 4x6 is. At this stage we’re not confident with either the 4’s or the 6 times table. But what we can do is work out that 2x6 is 12.
If we have another set of 2x6, that would be another 12.
Now, if we add both of those 2 groups of 6 together (12+12) we would have 4 groups of 6, 4x6 giving us the answer 24.
Another example: 4x8
2x8 = 16
2x8 = 16
2+2=4 (so 4 groups of 8)
16 + 16 = 32
4x8=32

How to support the 6x tables:
By the times we reach the 6x table we are already fairly confident with several of the times tables meaning that we can flip the question around and use our prior knowledge to work these questions out. However, as I will suggest with some of the other times tables, the 6’s can be supported by splitting the 6 and multiplying the number by 5 and then add one more group on.
I’ll explain this with an example: 6x7
6x7 is made up of 6 groups of 7.
We know that 5x7 (or 5 groups of 7) is 35.
If we add one more group of 7 onto that we will have 6 groups.
So, therefore 6x7 = 35+7 =42
I hope that makes sense.
Let me use a second example: 6x12
5x12=60
Plus one more group of 12: 60+12 =72
Therefore, 6x12=72

How to support the 7x tables:
The 7’s are regarded as the hardest of all the times tables, especially 7x8 (56). But I think by isolating one question like that it actually makes it easier to remember rather than taking it as one of many.
When you do come to tackle the 7’s, what I suggest you do is split the 7 into 5x and 2x and add your answers together.
For example, 8x7 becomes:
8x5= 40
8x2 =16
40+16 =56
Because, you have already gained confidence with the 5’s and the 2’s earlier on in your practice, this makes the 7’s much easier to confront now.

How to support the 8x tables:
You’ve made it to the 8x table, and you are hopefully confident with all the previous times tables. If that is the case, I would suggest the easiest way to approach the 8’s is to focus on what you are multiplying by 8 instead of the 8.
So, for example, if you are asked 4x8. You know your 4x table so you can work out 8x 4. From what you have learned previously you know that this is 32.
By changing the focus of the question, you will find that you know most of the answers all ready.
When it comes to 8x8 there is a rhyme that you may choose to share with your child. It’s gross but memorable:
I ate and I ate, and I was sick on the floor!
8x8 is 64

I ate and I ate
Until I was sick on the floor
8x8=64

How to support the 12x tables:
Because 12, is such a large number it is once again regarded as one of the harder ones to learn. But if we once again split the 12 into a 10 and a 2, we could make it much easier to work out the answer:
For example, 6x12 becomes:
6x10= 60
6x2 = 12
60+12 =72
Because, you have already gained confidence with the 10’s and the 2’s earlier on in your practice, this again makes the 12’s much easier to deal with now.
Never be afraid of writing things down. A lot of children (boys especially) seem to like to tackle the questions in their heads. However, they are far more likely to get it right when they can see the methodology written down. If there are any mistakes you can also see where they are occurring, making it easier to reflect back and correct them/ highlight where they are going wrong and the area that needs to be worked on a bit further.
Simple games I would suggest supporting the times tables
Having tricks to support the times tables are great, but to concrete that knowledge in our mind we need to practice. Your initial question was there a way to do it without just repeating them over and over again.
So, these are 4 quick and easy games that I use that you too will hopefully enjoy and find useful in practicing the times tables.
Noughts and crosses/tic-tac-toe
This game is great because it literally takes seconds to create and seconds to play/ destroy your opponent!
(Having said that, if one of your goals is to boost their confidence, it may be advisable to let them win sometimes. Having said that, you will quite possibly find they destroy you each time with out that being your intention…)
Start by drawing a noughts-and- crosses’ grid. 2 vertical lines crossed by 2 horizontal lines.
Into each square you have created place a number from 1-12.
That is the playing board created.
Now to play, decide which times table you are focusing on.
Let’s imagine you choose the 6x table.
In the centre square a 4 is written. To claim that square I must multiply the 4 by our focus times table, 6.
5x4=20
1x4=4
20+4=24
It is now your turn; you choose the top left where a 10 is written. You jump straight in with the answer 10x6=60.
The goal is simply to get a line of 3 correct answers before your opponent does.

A simple times tables (noughts and crosses) game
Jenga
I love this game but be prepared to be frustrated when you can see the tower wobble, but you have started to take your brick. You are passed the point of no return. You know you are about to lose but there is nothing at all you can do about it.
It’s devastating.
I came up with the idea as I was researching how to support a child with handwriting. However, I didn’t feel I could turn up and just start playing Jenga as I didn’t know the family that well at the time.
So, on each brick I wrote a simple word. My idea was that once you had removed the brick you would write the word in your very best handwriting, then as he got more confident, we started putting the word into a sentence. However, it struck me that if I was to put a number onto each brick, we could easily use the bricks for more opportunities.
So, in this instance what I suggest is that you write a number from 2-12 on each brick. Again, decide which times table you are focusing on.
This time as you remove the brick multiply the number written on the brick by your chosen times table. Once correct place the brick back on the top of the tower.
The next person then has a turn.
Whoever causes the tower to fall loses.
Enjoy!
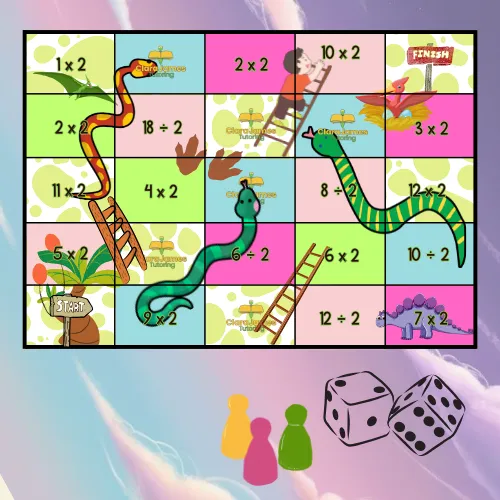
Using Jenga to help practise the times tables in a fun way
Lily pads
I call this game lily pads because when I originally came up with the idea, I envisioned using the frogs that jump that you get inside crackers. (You press on their backs, and they leap). However, I never had much joy in getting them to jump. That is clearly not where my skills lie.
So instead, I decided to adapt the game and play it like tiddly winks instead.
On 12 pieces of paper (not too big, probably about the size of the base of a cup) write a question from your focus times table. One piece of paper will say 1x4, for example. The next will have 2x4 written on it, etc.
Spread them out on the table in front of you.
Each player needs 2 counters.
Hold the second counter between the thumb and the index finger. Now press the counter down quite hard onto the very edge of the other counter.
That should cause it to jump forward.
It might take one or two practice goes.
Once confident in this part, take it in turns to aim for the piece of paper.
If your counter lands on one of the questions you answer it, then put it to a side.
If you miss, leave your counter where it is and the other person has a go.
The person who claims more questions, wins.

The times tables lily pad game
Where can I find more help?
I could talk about this all day and give you more ideas of games you could play.
If you’d like more fun, practical ways to help your child learn their times tables, my themed times tables books are packed with games and activities. There’s a dinosaur-themed version for dinosaur lovers, a fairies-themed version for those who prefer fairies, and a general themed book too — all available on Amazon.
Copywrite: Clara James Tutoring 2025



